Parallel transport maps on the Chiang Lagrangian.Abstract
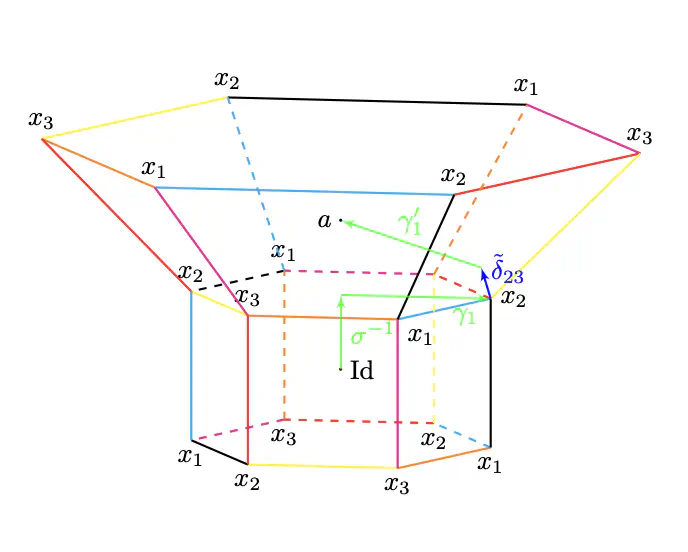
We extend Floer theory for monotone Lagrangians to allow coefficients in local systems of arbitrary rank. Unlike the rank 1 case, this is often obstructed by Maslov 2 discs. We study exactly what the obstruction is and define some natural unobstructed subcomplexes. To illustrate these constructions we do some explicit calculations for the Chiang Lagrangian $L_{\Delta} \subseteq \mathbb{C}\mathbb{P}^3$. For example, we equip $L_{\Delta}$ with a particular rank 2 local system $W$ over $\mathbb{Z}/2\mathbb{Z}$ for which the resulting Floer complex $CF_{∗}(W, W)$ is unobstructed despite the presence of Maslov 2 discs. We compute that the cohomology $HF_∗(W, W)$ is non-zero and deduce that $L_{\Delta}$ cannot be disjoined from $\mathbb{R}\mathbb{P}^3$ by a Hamiltonian isotopy.
